Las Matemáticas como una de las materias que nos enseñan en la educación básica y secundaria, incide directamente en nuestra forma de percibir nuestro entorno y sobre la manera de resolver los eventos (problemas o ejercicios matemáticos) que se nos presenten en nuestro trabajo como Ingeniera. Lo menciono porque uno de los temas que me gustaba mucho fue el de polinomios, partiendo con los monomios (X³), que a pesar que tiene el exponente igual a 3, se trata de una expresión con 1 término. Cuando se tienen 2 piezas, números, letras o términos se les nombra como binomios, por ejemplo: (M + n), sin distinción que pueden ser mayúsculas o minúsculas.

Cuando se utilizan números y letras, estamos seguros que el tratamiento matemático se basa en el cálculo de expresiones algebraicas, por lo que tenemos que familiarizarnos con las operaciones entre monomios, binomios u otros polinomios. Veamos el siguiente ejemplo:

(2X³)×(5X²) = (2×5)×(X³×X²) = 10X⁵

Y es aquí donde el proceso de enseñanza-aprendizaje mueve el piso del estudiante que comienza a preguntarse: "si multiplicamos 1 monomio por 1 monomio, ¿no debería resultar 1 monomio al cuadrado? o tal vez un binomio.

Vamos paso a paso, ahora incrementemos el producto de 1 monomio por 1 binomio, para ver si llegamos al resultado de una lógica matemática como la que se plantea en el párrafo anterior.

(2X³)×(5X² + 3X³) = (2×5)(X³×X²) + (2×3)(X³×X³) = 10X⁵ + 6X⁶
Va tomando un patrón que parece lógico, monomio por monomio resulta 1 monomio, mientras que monomio por binomio da como resultado 1 binomio, es decir el que tiene mayor términos.

Sigamos extendiendo el cálculo algebraico para 2 expresiones binomiales y su producto debería ser 1 binomio, o tal vez de mayor términos. Veamos el siguiente ejemplo:

Lógica matemática:

se plantea una premisa que debe ser probada en repetidas ocasiones para presentarla como válida, siguiendo el razonamiento matemático que el producto de 1 binomio por 1 binomio resulta ser 1 trinomio (expresión algebraica de 3 términos).

No se cumplen los criterios planteados anteriormente, ya que el resultado es un cuatrinomio, polinomio de 4 términos en lugar de 3, como resultó en el ejemplo anterior (trinomio). Así que no es predecible afirmar que el producto de multiplicar cualquier tipo de binomio puede ser trinomio, cuatrinomio u otro polinomio.

Lo que sí está establecido en el cálculo de expresiones algebraicas es que el cuadrado de un binomio, visto como la multiplicación de 2 binomios con términos similares, resulta inequívocamente en 1 trinomio.

Cuadrado de un binomio

Como la regla propuesta no se cumple un 100% para el producto de monomios y binomios, no nos puede desilucionar, ya que las Matemáticas precisaron una terminología más convincente: Producto Notable, para referirse a casos particulares donde se obtiene una expresión algebraica que se cumple siempre. En el caso que les presento aquí, me referiré al producto notable: (M + n)×(M + n)

Ahora sí, bajo estas condiciones, el producto de 2 binomios semejantes da como resultado 1 trinomio (no 1 cuatrinomio u otro tipo de polinomio). Además, se cumple que el primer término del producto es el cuadrado del primer término del binomio, el segundo término del trinomio será el producto del primer término del binomio por el segundo término del binomio, a la vez que se multiplican por 2, y finalmente el tercer término del trinomio es el cuadrado del segundo término del binomio. ¿Te resultó fácil expresar el resultado de este producto notable?

Una aplicación directa de esta expresión algebraica es la determinación del área de un cuadrado de lados iguales (por supuesto), pero medidos en 2 longitudes para expresarlas como un binomio. Para esta explicación voy a utilizar la figura del cuadrado mostrado anteriormente.

Note que la sumatoria de los 2 cuadrados internos más los 2 rectángulos internos, dan como resultado el área total del cuadrado de lados (M + n). Tal como se había desarrollado el producto notable: (M + n)×(M + n) es igual al cuadrado del binomio, (M + n)² = M² + 2Mn + n²

¿Qué sucede en el caso que el binomio sea una resta?

Debemos desarrollar el producto notable: (M - n)×(M - n) para obtener el producto del cuadrado del binomio.

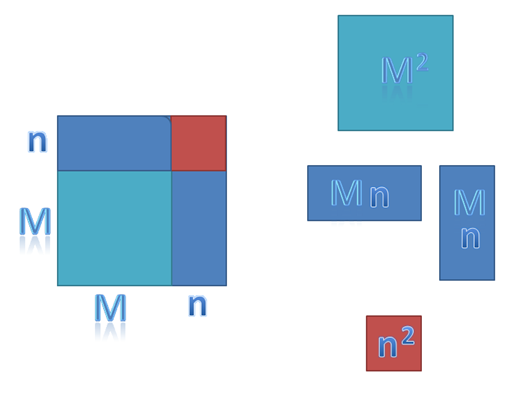
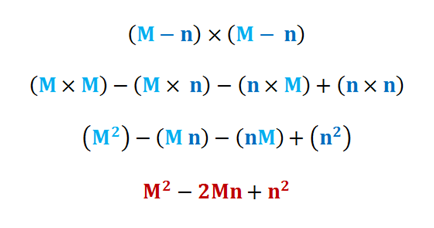
Nuevamente, el resultado del producto notable de 2 binomios es 1 trinomio. La regla de los signos aplica en esta expresión algebraica y aparece el signo negativo en el segundo término, esto es invariable por tratarse de un producto notable.

Área de un cuadrado:

se tiene un cuadrado de lado M al que se le sustrae una porción igual a n, por lo que el binomio queda expresado como: (M − n) y su producto (M − n)(M − n). Representemos gráficamente el área de los cuadrados y rectángulos internos para el producto notable del cuadrado de un binomio (caso resta):

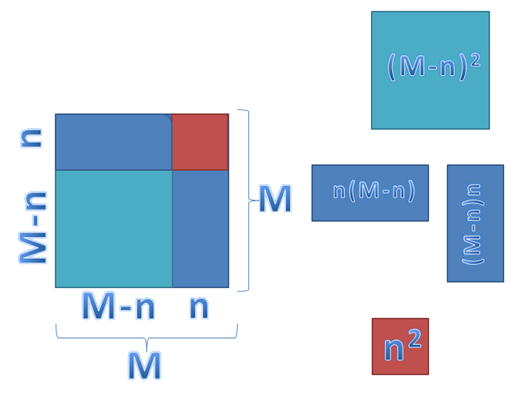
El área total del cuadrado es lado M por lado M que es igual a M². La sumatoria de las figuras geométricas internas será:

Veamos el siguiente ejemplo: Sea un cuadrado de lados L = 8 cm, que se reparte en 2 longitudes: M = 6 cm y n = 2 cm. Calcule el área total, el área de los cuadrados y rectángulos mostrados en la siguiente figura geométrica:

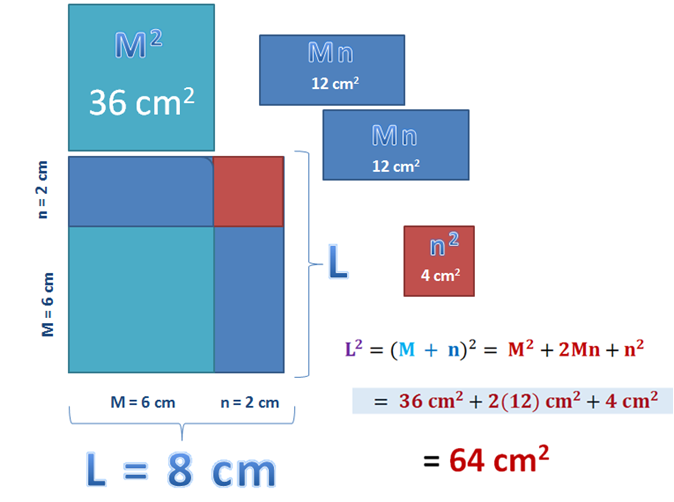
Aquí podemos aplicar lo que hemos desarrollado sobre el producto notable (M + n)×(M + n), el cuadrado de un binomio (M + n)² y lo que sabemos acerca del área de un cuadrado (A_▢ = L²)

Como L = 8 cm, entonces el área del cuadrado es A_▢ = L² = (8 cm)² = 64 cm²

El área de cada sección geométrica se obtiene de esta manera:

Apoyo bibliográfico y fuente de imágenes

Nuestra lógica y razonamiento matemático pueden ampliarse de manera voluntaria al consultar el siguiente catálogo de referencias:

• Imagen de geralt: Portada sobre Área y Binomios
• Blog: Reconocer e Identificar Monomios, Binomios y Trinomios
• Figura de fondo: Diseño de cubo (Pexels)
• Blog: Las identidades notables

Las identidades matemáticas son expresiones algebraicas
que facilitan el cálculo de magnitudes susceptibles
a ser medidas, como el área de un terreno o una figura geométrica