How I programmed a solver for the knight and bishop checkmate

^{Me, playing chess with my son who usually beats me}

In 1999, I programmed a solver for the knight and bishop checkmate. I had not seen that done before. I talked about that in my last post. A few people asked me to talk a little about my algorithm.

In those days, it really caught my attention that some strong chess programs didn't solve the problem and took too much time to analyze a knight and bishop endgame. I thought: "why?, how difficult could it be to include all the answers of known endings inside the program, so it doesn't lose time thinking. Getting all those answers must be easy if we're talking about only four pieces over the board".

Easy?... Really?...
Yes, of course.
I was sure about that.

First, we must find out how many positions we're talking about.
That's easy: 64 squares and 4 pieces:

64⁴ = 64 x 64 x 64 x 64 = 16777216 (beautiful number for programmers).

That's a start.

We have thus clearly defined the limits of this universe. Now we know how many different ways a white king, a white knight, a white bishop and a black king can be arranged over the chessboard. The value 16777216 includes a number of invalid positions (i.e. two or more pieces in the same square) but we can manage that later.

See the image:

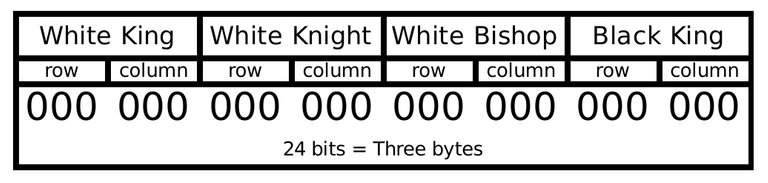
Those 24 bits are going to be used to orderly go through all the positions. Any four pieces chess position can be represented using a Long Integer. We need only three bytes but in my program I used a four bytes integer (Long Integer). The variable Position is a Long Integer.

See this simple but powerful code:

For Position = 0 to 16777215
   Mark_Position_As(32) 'Not yet solved 
Next

Do
   For Position = 0 to 16777215
      if Not_Valid(Position) then Mark_Position_As(0): break
      if Winning_Possible(Position) then Mark_Position_As(Move_Number): break
      if Mate_in_Zero(Position) then Mark_Position_As(30): break
      if Draw(Position) then Mark_Position_As(31): break
   Next
Repeat Until No_More_Changes_In_Solutions

The above code is the basic structure that solves the problem, it finds all the solutions for the knight and bishop checkmate. All the solutions should be saved in a file with a size of 16777216 bytes (one byte per answer) . Out of this code, everything should be easy to infere. Let me explain a little the works done by the functions Not_Valid, Winning_Possible, Mate_in_Zero and Draw.

NOT_VALID
A position is not valid when:

1. Two pieces are in the same square.
2. The kings are in adjacent squares.
3. Black is in check but not checkmated (Remember: It's always white's turn to move).

WINNING POSSIBLE
Here we check if one of the available moves put the black king in checkmate or force it to another position already marked as Winning_Possible. Every move available must be given a value. The values of Move_Number range from 1 to 29, being 29 the maximum possible number of moves with a knight (8 moves), a bishop (13 moves) and a king (8 moves).

MATE_IN_ZERO
In the position the black king is already checkmated.

DRAW
The position is a draw when:

1. The black king is stalemated.
2. All available moves leads to stalemate or losing a piece.
   ^{(Now I know there are only 39 positions where the stalemate or the loss of a piece are unavoidable).}

This is pretty short and pretty simple (and pretty powerful).
If you see closely, you may realize that you can use it to solve any four pieces ending.

May be I omitted something. I tried to keep it short. Let the questions come.

Greetings from Venezuela.